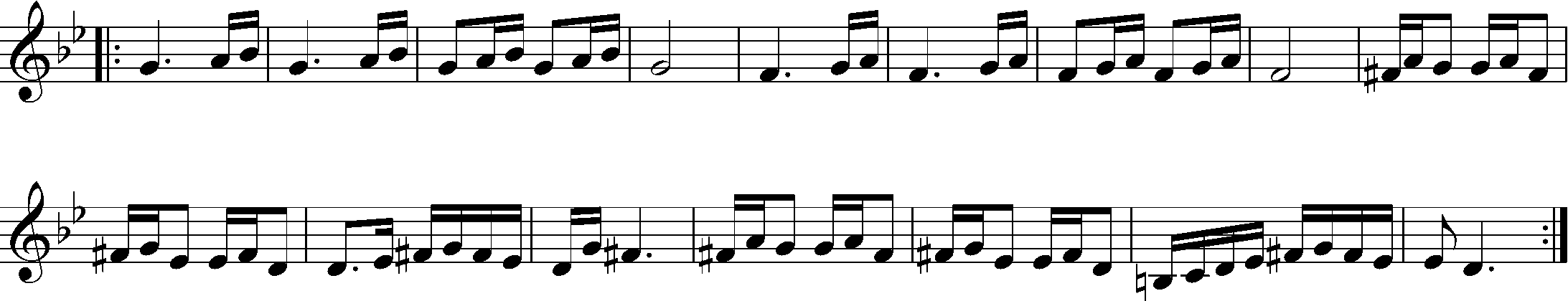TUNE OF THE MONTH: Taniec Rabina/Der Chosid Tantzt/Flaskadriga/Dem Rebens Tanz

This series begins with what I consider one of the most interesting tunes in the klezmer repertoire.  The earliest recording of it that I have heard is “Taniec Rabina” (Rabbi’s Dance) by the Belf Orchestra, recorded in Roumenia in 1912.  

In this iteration it is a simple, two section tune in which the second section is essentially the first section raised up a third:

The Belf performance is of particular note because they take this very simple tune and play it entirely over the root chord – in the version notated here, that would be D major.  There is no cadence chord, which is extremely unusual.  Instead, the piano player employs a huge vocabulary of rhythmic variation to keep things interesting.  The net effect is to conjure up the hypnotic, almost mystical image of a Chassidic rebbe dancing.

In 1920. Lt. Joseph Frankel recorded an intriguing version of this tune on Emerson under the title, "Der Chosid Tantzt part 1."  Unlike the main body of his commercial recordings, which feature a large band, both sides of this disc feature Frankel himself on clarinet and an unknown accordion player.  In Frankel's version, the A and B sections are virtually identical to those of "Taniec Rabina," with a few small rhythmic variations.  The accordionist does change chords, but his choices appear to be a bit random, as was often the case during these early years of recording. Then there is an added C section:

Alert readers will perhaps recognize this melody.  The first four bars are virtually identical to the first four bars of the C section of another Belf tune, "Nakhes fun Kinder,"  

while the last four bars are absolutely identical to the end of the C section of a tune Frankel had recorded with his band the previous year, "Dem Rebin's Nigun, Oj Tate."

While it might seem that this is a random mish-mosh that proves the claim that all klezmer tunes sound alike, the connections among these melodic segments are actually strong.  The rhythmic change in the first four bars alters the Belf melody to reflect the thematic rhythm pattern of the A and B sections, the recurring four sixteenths followed by an eight note.  The part of the melody borrowed from "Oj Tate" shares that same recurring pattern.  The net result is a cohesive, organic tune.

In 1921, Harry Kandel recorded another version of this melody for the Victor label under the title “Flaskadriga”.  In this rendition the A and B sections are identical to the previous two versions, and like the Frankel, there is an added C section:

After the shout chorus, which is deceptive in that unlike the usual shout chorus, it neither establishes a new tonal center for the time (Gm would be what you might expect, based on the first four bars of the section) nor modulates into a new mode (F major, as indicated by the second four bars).  Instead, the shout chorus is just an interesting interlude that snaps immediately back to the starting tonality, while the melody itself echoes the very distinctive rhythmic figures of the first two sections of the tune.

The last iteration of this tune, "Dem Reben's Tanz," was recorded by Art Shryer in 1929. This recording is particularly interesting because of the spoken introduction, which sets the stage for the joyous spectacle of the Rebbe dancing.  In addition, every time it comes around, the A section includes a large chorus of voices singing the tune in the style of a Chassidic nign, which references the title in a much more literal way than the hypnotic playing of the Belf orchestra.

 The first half of the A section is identical to that of the previous three versions, but then, although it maintains the same rhythmic figure, the tune goes off in a completely different direction: 

 The next section of the tune, while evolving organically from the A section, bears much less resemblance to the original.  The only hint is a rhythmic echo in the sixth measure:

The C section returns to the rhythmic figures of the A section (and of the original tune) but resolves into very new territory:

 The final section of “Dem Rebens Tanz” slows the rhythm to eighth notes but builds dramatically to a fitting resolution:

Lead sheets for these four tunes can be found here:

Taniec Rabina

Der Chosid Tantzt pt 1

Flaskadriga

Dem Rebens Tants

They are also accessible from the Resources section of this web site, as are downloadable versions of the complete audio for each.

Barukh Habo (Welcome)!

Welcome to the new Klezmer Academy blog. This will be a place for sharing information, opinions and experiences about all aspects of klezmer music. I hope that in addition to being a platform for me to express my views and knowledge, it can also serve as a forum for discussion among other performers, educators and interested audience members.

One very special feature of the blog will be “Tune of the Month” posts. On the 15th of each month, I’ll publish a post about a tune I find particularly interesting. These might be unusual, rarely heard tunes from the Mayrent Collection, tunes that have been recorded by several groups in various geographic locations or at different time periods, or tunes with interesting modal, harmonic or structural elements. Each such post will include sound files of the recording(s) being discussed as well as a downloadable chart of the basic tune.

I am very interested in including reviews of recordings as well as descriptions/discussions of projects involving klezmer. If anyone would like to send me recordings to consider or would like to share information about current activities that might be of interest, please contact me at sherry@klezmeracademy.com. I would also welcome suggestions for guest posts by my colleagues.

Klezmer is the richest, most complex musical world that I know, and I look forward to exploring it in the months to come.

It's Not Jewish Jazz

Despite the worldwide revival of klezmer music over the past 30 years, many people don't know what it is or where it comes from. One commonly heard response to "Well, what is klezmer, anyway?" is that it's "Jewish jazz." While this answer is catchy and usually satisfies the questioner, it isn't actually true, and considering some differences between klezmer and jazz may help clarify matters.

Klezmer music, which can be most easily defined as the dance music of the Yiddish-speaking Jews of eastern Europe, is essentially communal, like Jewish prayer, rather than individual. The Yiddish word klezmer is derived from two Hebrew words: kley, which means tool or vessel, and zemer, which means song. Thus, as one famous klezmer has said, the musician becomes the vessel through which song flows, a concept that most jazz lovers would find quite congenial. It is, however, a very modern, not terribly authentic notion. In fact, kley is a word that resonates loudly in Yiddish culture. There is a wonderful term in Yiddish for those members of the community who performed ritual functions: kley koydesh, or holy tool. These included the shoykhet (kosher slaughterer), the moyl (performer of circumcisions), the rabbi, etc. These people were tools of the community. So was the musician, without whom there could be no weddings, no celebrations of Simkhes Toyre, no post-briss partying.

The music itself is an exciting mixture of prayer modes (nusakh) and melodies, Ukrainian folk tunes, Romanian music, gypsy soulfulness, and dozens of other influences of the cultures among which Jews lived, all played to the rhythms and inflections of spoken Yiddish. It expresses the whole range of human emotions, from the most exuberant joy to the most profound sadness. Melody is the key; unlike jazz, where a melody is improvised over a fixed set of chords, in klezmer music, the melody is fixed, and the chords are almost unnecessary. Rather than improvising, the musicians take the melody, embellish it in a large variety of ways, polish it up a little, and offer it back to the community to listen or dance to. Where jazz is laid back, always a little behind the beat, klezmer rushes ahead, which is part of what makes it so hard to sit still while you listen to it.

Another misconception common in the general public, even among those who are relatively familiar with Jewish culture, is that there is one universal klezmer band to which all klezmorim belong, or at least that all klezmer bands play a uniform style. In fact, there is a whole spectrum of stylistic approaches to Yiddish music, ranging from the most traditional to the most avant garde, with a shmaltzy, nostalgic approach lying somewhere in the middle. There are groups that virtually replicate the sound of old 78 rpm recordings, down to the instrumentation and even the mistakes; there are others that improvise Yiddish melodies to a hard rock beat, while still others attempt to merge Yiddish and jazz.

What klezmer does share with all other kinds of music is the ability to express the whole range of human emotions, from the most exuberant joy to the most profound sadness. Listening to the haunting, exhilarating sounds emanating from scratchy old 78s can be a profound experience, capturing the essence of Eastern European Jewish life in the last century and introducing it to a new generation.